不知道在想什么，也不知道要干什么，只是一些胡思乱想。

我现在在机房里，是的，我曾经轰轰烈烈的写了一页纸，控诉 OI，控诉我的人生，但是还是成为我最讨厌的样子，呆在机房里。

我不知道为什么。

浅谈前缀和与差分

一.前缀和

我们先抽象地说一说，对于一个数列 $a_n$，我们定义它的前缀和数列 $S_n= \sum _\limits{i=1}^{n} a_i$。

很好理解吧？我们再举个具体点的例子。

对于数列 1 2 4 5 3，它的前缀和就是 1 3 7 12 15。

那么如果你会了这个问题，那么现在请问：

• 例 1：给定数列 $a_n$ ， $q$ 组询问，每次读入整数 $l,r$ ，求 $ \sum _\limits{i=l}^{r} a_I$ 。 $(n,q \le 10^6)$

怎么做呢？

如果暴力每次都循环一遍求出和的话时间复杂度就会达到 $\Theta(n^2)$，不能接受。

为什么复杂度这么高呢？

对于一个子段，我们的答案是不变的，但是我们却进行了多次计算。

怎么办呢？

我们发现答案就是 $S_r-S_{l-1}$。请感性理解。

• 例 2（luogu P1147）：对一个给定的自然数 $M$，求出所有的连续的自然数段（每一段至少有两个数），这些连续的自然数段中的全部数之和为 $M$。$(M \le 2\times 10^6)$

这里我们想，我们这个前缀和有点特殊，具体怎么特殊呢？请看图：

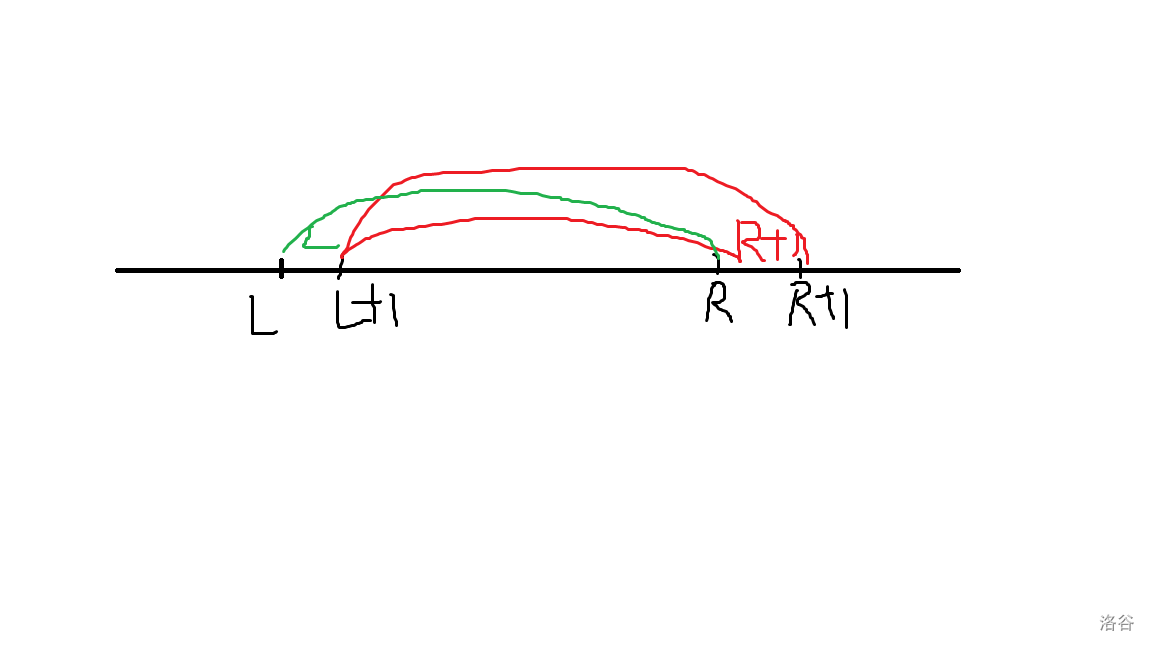
我们发现，当 $R$ 增大时，答案（也就是区间和）一定增加，当 $L$ 增大时，答案一定减少。

那么如果我当前答案比需要的答案 $M$ 少，我只能往右尝试着取 $R+1$，反之我只能扔掉 $L+1$，直到 $R$ 本身大于 $M$。

时间复杂度是什么呢？

可以证明：时间复杂度是 $\Theta(n)$，为什么？

这就是前缀和的思想，具体来说就是区间相减区间相加。

相信大家都很好理解，我们现在再来探究一下前缀和的本质？

• 思考：我们运用的什么性质导致前缀和的成立？

满足区间可减性与结合律，前者是可以算出起点不为 $1$ 的区间的条件，后者是本质条件。

（什么意思呢？前缀最大值能否推出区间最大值？但是它能解决什么问题？）

满足区间可减性的不止有 $+$，还有：

$\times$ 、$\operatorname{xor} $、 矩阵乘法、向量加法等等，所以前缀的不一定是和。

二.差分

对于一个数列 $a_n$，我们定义它的差分数列 $d_i= a_i-a_{i-1}$，特别地： $d_1=a_1$。

那么显然差分数列的前缀和就是原数列。

只不过是把加变成减了而已。

那差分有什么性质呢，请大家自己探究。

• 例 2（ CSP-J 2022 SD补测）：$q$ 次区间加操作，最后询问数列的最大值。$(1\le q\le 10^6)$

我们很容易发现如果对一个数列区间加 $x$ 等价于对它的差分数列 $d$ 进行 $d_l+x$，同时$ d_{r+1}-x$（想一想，为什么）？

那么差分也很好理解。

差分一般会结合数据结构考察，这里略去例题，但一定要注意，这是处理区间加的一种有力手段。

三.二维前缀和

定义二维数组 $a_{ij}$ 的前缀和 $S_{ij}$ 为 $\sum \limits_{l=1}^{i} \sum \limits_{r=1}^{j} a_{lr}$。

抽象的话就上图。

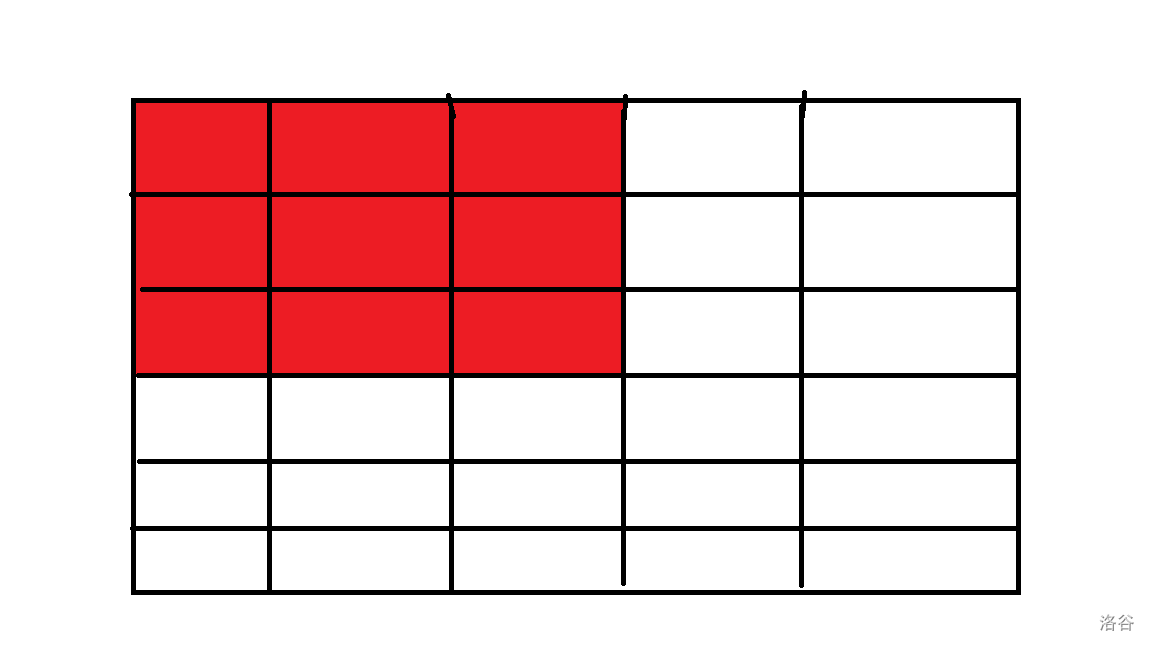
$S_{33}$ 就是图上标红的地方。

怎么求呢？

容斥原理！我们假设知道了所有小于 $i,j$ 的前缀和，那么看图来说：

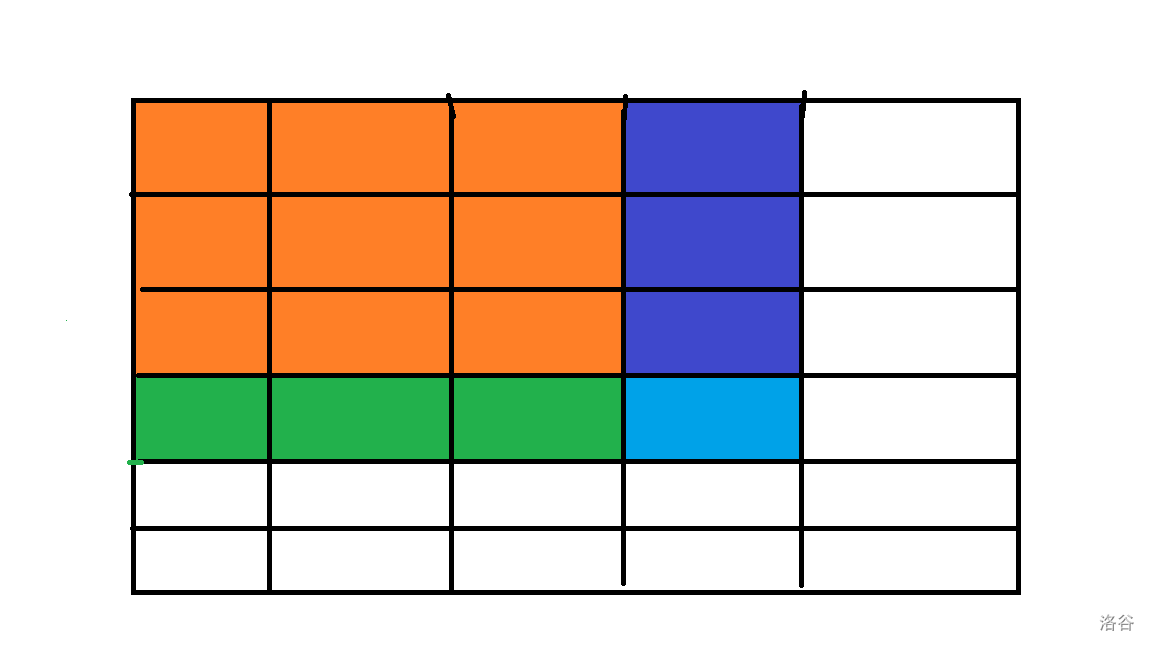
就是绿色+橙色+紫色+蓝色。而橙色就是 $S_{33}$，绿色就是 $S_{34}- S_{33}$，紫色就是 $S_{43}-S_{33}$ 。

题意简述

实现四种字符串操作，具体请看题面。

一.题意简述

现在有若干个数，值域为 $[1,n]$ ，其中大小为 $i$ 的数有 $a_i$ 个，现在重排这个序列使得前缀众数之和最大。

众数在这个题定义为：数列中出现最多的数，如果有出现次数一样的以最大的为众数。

植树节(planting)

一.一句话题意

区间加一，求序列最大值。

二.题目分析

一.线段树模板

略。

二.差分

定义：设原数组 $a_n$，设数组 $b_n=a_n-a_{n-1}$ 为 $a$ 的差分数组。其中一个性质是 $b$ 的前缀和数组就是 $a$。

我们很容易知道对 $a$ 任意区间 $[l,r]$ 区间加 $x$ 就等价于 $b_l + x$ 同时 $b_{r+1} -x$
证明略，请感性理解

三.代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		int l,r;
		cin>>l>>r;
		l++;r++;
		a[l]++;a[r+1]--;
	}
	for(int i=1;i<=1e6+4;i++){
		a[i]+=a[i-1];
	}
	int maxn=-1;
	for(int i=1;i<=1e6+4;i++){
		maxn=max(maxn,a[i]);
	}
	cout<<maxn<<endl;
}

宴会(banquet)

一.一句话题意

给定一个长为 $n$ 的序列 $a_n$ 和 $b_n$，求一个 $x_0$ 使得最小化 $\max_{i=1}^n{b_i+|x_i-x_0|}$。

二.题目分析

按照我们小学数学的知识，我们怎么处理绝对值问题呢？

其中一种解法就是几何意义：

我们先对这个式子进行等价变形，那么就有：

有点抽象？没关系来张图：

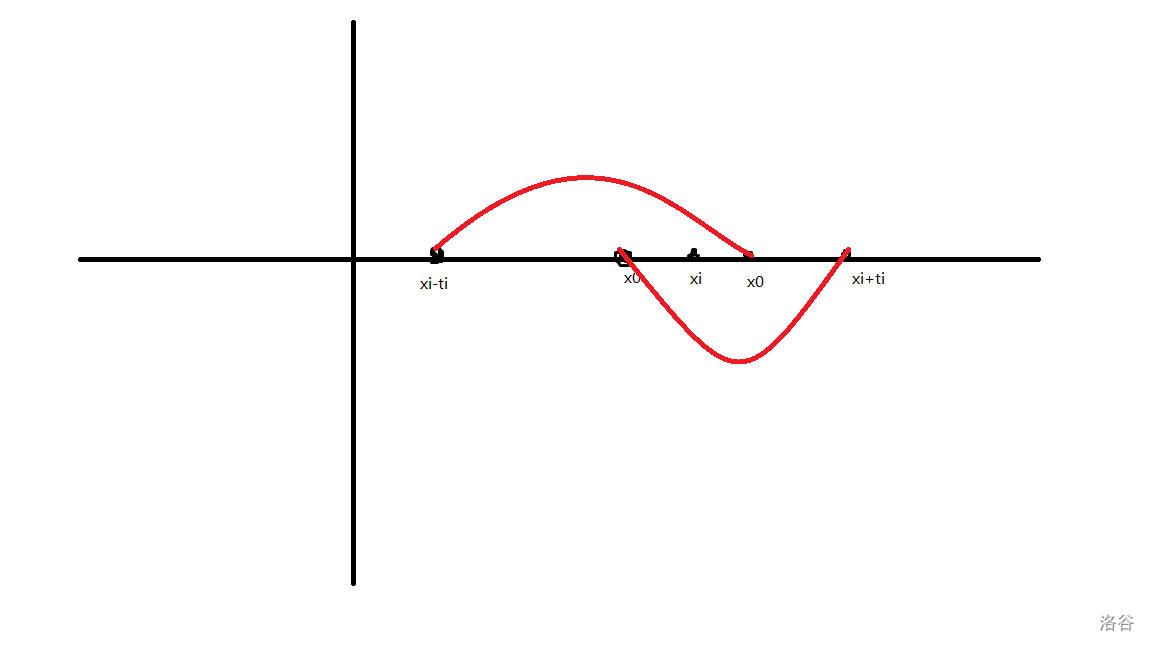
也就是说如果 $x_i<x_0$ 的时候，我们的 $d$ 就是右边红色的部分，否则就是左边红色的部分。

那么我们现在要让最大的 $d$ 最小 ，首先我们还是要找出这个 $d_{min}$。

那我们不妨找出值域，来看这样一张图：

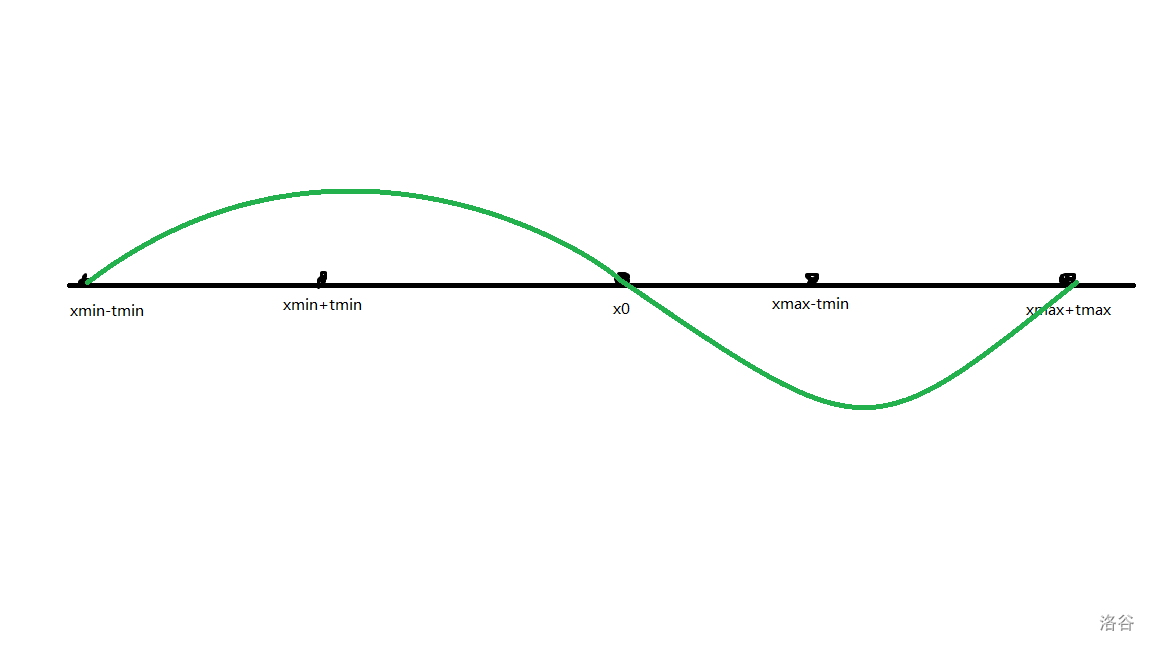
那么显然值域就是 $[x_{min}-t_{min},x_{max}+t_{max}]$。

那么显然当 $x_0$ 取值域终点的时候 $d=d_{min}$，即当 $\frac{x_{max}+t_{max}+x_{min}-t_{min}}{2}$ 即可。

代码时间

1
2
3
4
5
6
7
8
9
10
11

void solve(){
	read(n);
	for(int i=1;i<=n;i++)read(a[i]);
	for(int i=1;i<=n;i++)read(t[i]);
	int minn=INF,maxn=-1;
	for(int i=1;i<=n;i++){
		minn=min(a[i]-t[i],minn);minn=min(a[i]+t[i],minn);
		maxn=max(a[i]-t[i],maxn);maxn=max(a[i]+t[i],maxn);
	}
	printf("%.1lf\n",(minn+maxn)*1.0/2);
}

部署(deploy)

基础树论板子题。

一.题意简述

给定一棵树，两种操作：

1. 子树加
2. 父亲和儿子加

先进行操作，最后若干次单点询问。

二.题目分析

当我刚看到这道题的时候，我说：“这不是树剖板子？”接着我再看了一看发现不是，而且比树剖简单了不知道多少倍，毕竟是普及组的题目。

我们发现我们是修改完再查询，题目都把离线拍到了脸上。

考虑预处理操作最后再改，即最后只遍历一遍就可以知道所有点的权值。

首先是子树加，我们直接定义一个数组 $Sz_i$ 代表以 $i$ 为根的子树上加了多少，然后预处理就直接加就可以。

再接着是父亲和孩子的和，原题目给的是直接相连的点，但是这是一棵树，我们就要想一想树的特殊性质：树只有一个父亲、若干个儿子。

那只有一个父亲我们直接把父亲加上就好。

孩子呢？我们还知道树是一种递归结构，在这个题中就是指这些孩子都以这个节点为父亲。

那我们直接记录父亲加了多少，最后一遍 DFS 就可以知道每个点最后权值是多少了。

三.代码时间

• 注意双向边别忘了开 $2$ 倍数组。
• 题目中指定了 $1$ 号节点为根节点。
• 代码只给出了核心部分。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

/*
	Author:zd
	Status:WA on pretest 2
*/

void dfs1(int x,int f){
	fa[x]=f;
	for(int i=head[x];i;i=e[i].nxt){
		int y=e[i].to;
		if(y==f)continue;
		dfs1(y,x);
	}
}
void dfs2(int x,int tmp1,int tmp2){
	a[x]+=(tmp1+tmp2);
	for(int i=head[x];i;i=e[i].nxt){
		int y=e[i].to;
		if(y==fa[x])continue;
		dfs2(y,tmp1+sz[y],laz[x]);
	}
}

signed main(){
	read(n);
	for(int i=1;i<=n;i++)read(a[i]);
	for(int i=1;i<n;i++){
		int x,y;
		read(x,y);
		ade(x,y);
		ade(y,x);
	}
	dfs1(1,0);
	read(m);
	while(m--){
		int op,x,y;
		read(op,x,y);
		if(op==1){
			sz[x]+=y;
		}
		else{
			a[fa[x]]+=y;
			a[x]+=y;
			laz[x]+=y;
		}
	}
	dfs2(1,sz[1],0);
	read(k);
	while(k--){
		int x;
		read(x);
		writeh(a[x]);
	}
	return 0;
}

吟诗(poetize)

史上最难普及组题目

一.一句话简述不完题意

给定常数 $X,Y,Z$，求长度为 $n$ 的数列 $a(1\le a_i \le 10,1\le i \le n)$的个数， 使得存在 $1 \le x \le y \le z \le r $，使得：

是的我在尽量不抽象了。

二.题目分析

先想暴力。

显然有一个枚举全排列的暴力分，太过 $\color{red}\text{Native}$ 这里不说了。

$40$ 分呢？

我们想到去推柿子，但是问题是我们稍微写一写就发现我们直接这么做会出现重复计数的问题，并且这个问题还十分地棘手，怎么办呢？

我们发现总数量就是 $10^n$。正难则反，考虑解决不合法的数目，容斥原理即可。

然后便没有思路了，数学这条路算是堵死了。

再看一眼数据范围：$X+Y+Z \le 17 ,n \le 40$ 考虑状压 DP。

因为 $n$ 太大了我们考虑状压 $X+Y+Z$，现在的问题是设计一种状压方案储存一个不超过 $17$ 的数，同时还能快速判断条件是否合法。

我们考虑到把一个数 $m$ 拆成若干个有序正整数的方案数为 $2^{m-1}$ （想一想，为什么？），我们可以看成 $m$ 个 $1$ 相加，每一位中间可以选择分割或者不分割。受此启发，我们设计这样一种状态：第 $i$ 位若为 $1$ 说明在第 $i$ 位和第 $i+1$ 位之间选择分割，也就是说存在一个前缀和为 $i$ 。

然后我们再把它反转过来，变成后缀和，原因是我们 DP 是从前往后递推的，这样可以方便判断，具体来说，我们把 $17$ 分成 $5,7,5$，对应的压缩是 10000100000010000 ，从后往前数第 $5,12,17$ 位为 $1$，即存在 $5,12,17$ 的 后缀和。

怎么判断题意呢？只需要同时存在 $Z,Y+Z,X+Y+Z$ 的后缀和即可。

推一下柿子，当状态为 $i$时加入一个新数 $t$ 时，新的状态为 (i<<t)+(1<<(t-1))。

然后按照题意 DP 即可。

三.代码时间

• 注意位运算的优先级很低，一定要勤加括号。
• 一般这种题需要注意运算中爆 int ，本人习惯一般 #define int long long。
• 取模一定要勤快，不然你都不知道你这个数为啥这么奇怪。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

int n,m,k;
int f[45][N],X,Y,Z;
bool gb(int i,int x){
	return (x>>(i-1))&1;
}//取第 i 位 
bool check(int num){
	if(!gb(Z,num)) return 1;
	if(!gb(Y+Z,num)) return 1;
	if(!gb(X+Y+Z,num)) return 1;
	//后缀和判断是否不合法 
	return 0;
}

signed main(){
	read(n,X,Y,Z);
	f[0][0]=1;
	for(int i=1;i<=n;i++){//长度 
		for(int j=0;j<(1<<(X+Y+Z));j++){//枚举状态 
			for(int k=1;k<=10;k++){
				int u=(j<<k)+(1<<(k-1));//处理后缀和 
                u&=(1<<(X+Y+Z))-1;
				if(check(u))(f[i][u]+=f[i-1][j])%=mod;
			}//暴力填数 
		}
	}
	int ans=qp(10,n);
	for(int i=0;i<(1<<(X+Y+Z));i++)(ans+=mod-f[n][i])%mod;
	writeh(ans%mod);
	return 0;
}

不知道为什么和 THUPC 的那道众数这么像。

题意简述

有长度为 $n$ 的数列 $a_n,b_n$ ，对于每个位置 $i$，我们只能选择 $a_i$ 或 $b_i$ ，求选择的 $|a_{max}-b_{max}|$。$(1\le n \le 5\times 10^5)$.

现在是22年12月30日，距离22年结束已经不剩几天了。

有关于22年的一切，都显得如此的抽象与魔幻，似乎这种事情在前几年根本不会想到，但是它的确确确实实的在发生着，无论是快乐还是悲伤，它都在我们经过的一年中划过。

一年的时间，回过头看看还是这么长，似乎22年刚开始的时候，我还是那么幼稚，稚嫩，似乎12个月之后，我又学到了不少东西，当然，也失去了不少东西。我想，我的22年是“交换”的一年，交换观点，交换成败，交换曾经的日常生活，变成了现在所奢望的，而曾经看上去遥不可及的事物，不说触手可得，倒也不必仰望了。

22年的生活，被鲜明地化成三种不同的风格，也都有着难忘的记忆。在前半年，我居然还过着初中的生活，现在想想仿佛在上一辈子，似乎需要担心，“欢笑”成了它一提起来就想到的感情，和同学出去玩玩，去干一些之前想都没想过的事情，虽说大胆，也不过如此。渐渐地，还是步入了高中生活，而我的高中生活的开始，被竞赛彻底的占据，这也是我做出的最冒险的一个决定，在稳定与动荡，未来与过去之间，我还是选择了自己想选择的选项，至少，不管结果如何，我不后悔。

竞赛的三个月也是我记得最清楚的三个月，像是完全另一个世界，另一个我一样，没有了语文英语课文，没有了晦涩难懂的数学题，每天只是和数组算法打交道，学习自己最感兴趣的知识，和一群志同道合之友畅聊科技政治再到人生，最后在模拟赛中在“彼此处刑”。现在想想，有了这三个月，我也是值得的，不管得了什么奖，我还是没有虚度这三个月的光阴。

虽说如此，我还是带着遗憾回到了正常高中生的生活中，但是这生活又显得如此特殊，之前对于文化课都是不断寻求新知识，抱着对所谓文科的偏见，执着自己一点微弱的理科优势横冲直撞。现在却只能无比痛苦地承认自己哪一科听得也没有那么透彻了。更痛苦的是，也在这种自我折磨中发现了曾经的偏见是多么地幼稚可笑。

这便是我现在的2022，是我把生活重启转弯的一年。

这么奇妙的一年，终究还是会走到终点，曾经的什么遗憾与不舍，在现在也显得这么可笑，前路未必平坦，但是还是选择去勇敢面对吧。

23年，希望能少一点曾经的偏见，我并不一定是对的，相反，还很可能是错的。但是，心中认定是对的，也要这么继续做下去，走下去。未来一定会继续改变，我只希望等到一年后，看着现在我写下的这通文字，我能意识到，我23年一年并没有走弯路，我还是向着我想远航的方向没有偏离，最后对着这些文字嘲笑今年的幼稚。我也更希望我能干出想今年一样改变自己但不曾后悔的事情，不断地获取资源更好的提升自己，等到自己站到全新的高度之后再去接触全新的资源，这不就是学习的意义吗？

距离23年之后短暂的一天了，伤感只是属于过去逝去的事情，展望未来，也必定是鼓足了气力，不过，还需要迈出这坚实的一步，一步一步在现实中走向未来，

现在是22年12月30日，距离22年结束已经不剩几天了。

有关于22年的一切，都显得如此的抽象与魔幻，似乎这种事情在前几年根本不会想到，但是它的确确确实实的在发生着，无论是快乐还是悲伤，它都在我们经过的一年中划过。

一年的时间，回过头看看还是这么长，似乎22年刚开始的时候，我还是那么幼稚，稚嫩，似乎12个月之后，我又学到了不少东西，当然，也失去了不少东西。我想，我的22年是“交换”的一年，交换观点，交换成败，交换曾经的日常生活，变成了现在所奢望的，而曾经看上去遥不可及的事物，不说触手可得，倒也不必仰望了。

22年的生活，被鲜明地化成三种不同的风格，也都有着难忘的记忆。在前半年，我居然还过着初中的生活，现在想想仿佛在上一辈子，似乎需要担心，“欢笑”成了它一提起来就想到的感情，和同学出去玩玩，去干一些之前想都没想过的事情，虽说大胆，也不过如此。渐渐地，还是步入了高中生活，而我的高中生活的开始，被竞赛彻底的占据，这也是我做出的最冒险的一个决定，在稳定与动荡，未来与过去之间，我还是选择了自己想选择的选项，至少，不管结果如何，我不后悔。

竞赛的三个月也是我记得最清楚的三个月，像是完全另一个世界，另一个我一样，没有了语文英语课文，没有了晦涩难懂的数学题，每天只是和数组算法打交道，学习自己最感兴趣的知识，和一群志同道合之友畅聊科技政治再到人生，最后在模拟赛中在“彼此处刑”。现在想想，有了这三个月，我也是值得的，不管得了什么奖，我还是没有虚度这三个月的光阴。

虽说如此，我还是带着遗憾回到了正常高中生的生活中，但是这生活又显得如此特殊，之前对于文化课都是不断寻求新知识，抱着对所谓文科的偏见，执着自己一点微弱的理科优势横冲直撞。现在却只能无比痛苦地承认自己哪一科听得也没有那么透彻了。更痛苦的是，也在这种自我折磨中发现了曾经的偏见是多么地幼稚可笑。

这便是我现在的2022，是我把生活重启转弯的一年。

这么奇妙的一年，终究还是会走到终点，曾经的什么遗憾与不舍，在现在也显得这么可笑，前路未必平坦，但是还是选择去勇敢面对吧。

23年，希望能少一点曾经的偏见，我并不一定是对的，相反，还很可能是错的。但是，心中认定是对的，也要这么继续做下去，走下去。未来一定会继续改变，我只希望等到一年后，看着现在我写下的这通文字，我能意识到，我23年一年并没有走弯路，我还是向着我想远航的方向没有偏离，最后对着这些文字嘲笑今年的幼稚。我也更希望我能干出想今年一样改变自己但不曾后悔的事情，不断地获取资源更好的提升自己，等到自己站到全新的高度之后再去接触全新的资源，这不就是学习的意义吗？

距离23年之后短暂的一天了，伤感只是属于过去逝去的事情，展望未来，也必定是鼓足了气力，不过，还需要迈出这坚实的一步，一步一步在现实中走向未来，

看着题解区内没有双指针的做法，这里向大家介绍一下本题双指针的做法。