浅谈前缀和与差分

一.前缀和

我们先抽象地说一说，对于一个数列 $a_n$，我们定义它的前缀和数列 $S_n= \sum _\limits{i=1}^{n} a_i$。

很好理解吧？我们再举个具体点的例子。

对于数列 1 2 4 5 3，它的前缀和就是 1 3 7 12 15。

那么如果你会了这个问题，那么现在请问：

例 1：给定数列 $a_n$ ， $q$ 组询问，每次读入整数 $l,r$ ，求 $ \sum _\limits{i=l}^{r} a_I$ 。 $(n,q \le 10^6)$

怎么做呢？

如果暴力每次都循环一遍求出和的话时间复杂度就会达到 $\Theta(n^2)$，不能接受。

为什么复杂度这么高呢？

对于一个子段，我们的答案是不变的，但是我们却进行了多次计算。

怎么办呢？

我们发现答案就是 $S_r-S_{l-1}$。请感性理解。

例 2（luogu P1147）：对一个给定的自然数 $M$，求出所有的连续的自然数段（每一段至少有两个数），这些连续的自然数段中的全部数之和为 $M$。$(M \le 2\times 10^6)$

这里我们想，我们这个前缀和有点特殊，具体怎么特殊呢？请看图：

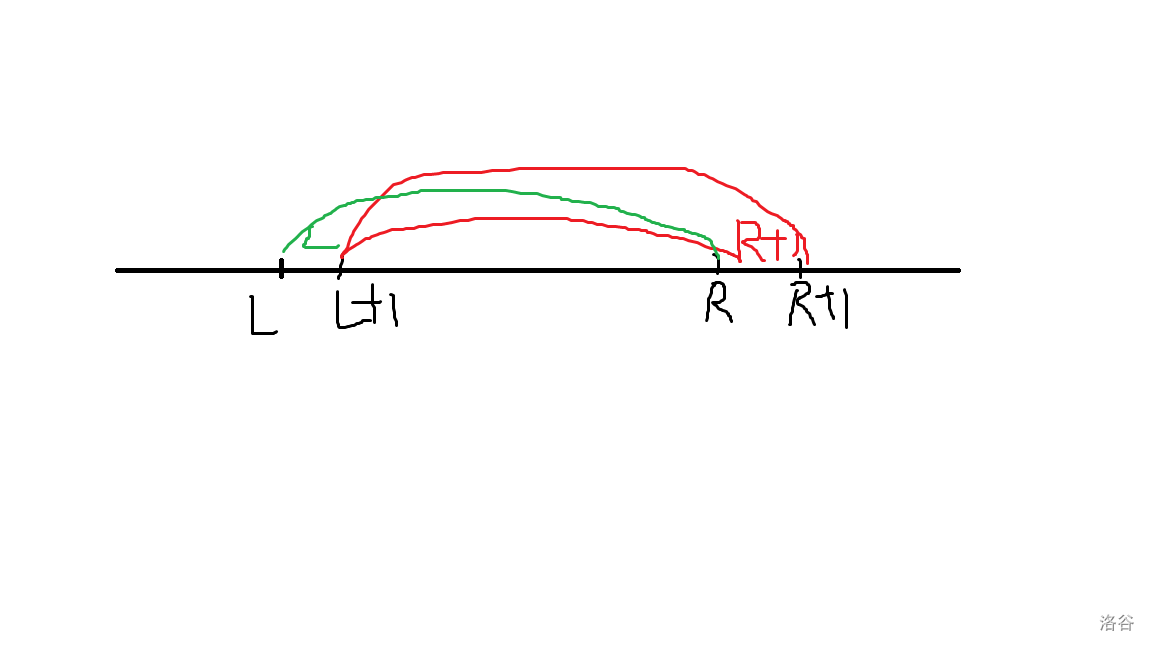
我们发现，当 $R$ 增大时，答案（也就是区间和）一定增加，当 $L$ 增大时，答案一定减少。

那么如果我当前答案比需要的答案 $M$ 少，我只能往右尝试着取 $R+1$，反之我只能扔掉 $L+1$，直到 $R$ 本身大于 $M$。

时间复杂度是什么呢？

可以证明：时间复杂度是 $\Theta(n)$，为什么？

这就是前缀和的思想，具体来说就是区间相减区间相加。

相信大家都很好理解，我们现在再来探究一下前缀和的本质？

满足区间可减性与结合律，前者是可以算出起点不为 $1$ 的区间的条件，后者是本质条件。

（什么意思呢？前缀最大值能否推出区间最大值？但是它能解决什么问题？）

满足区间可减性的不止有 $+$，还有：

$\times$ 、$\operatorname{xor} $、矩阵乘法、向量加法等等，所以前缀的不一定是和。

对于一个数列 $a_n$，我们定义它的差分数列 $d_i= a_i-a_{i-1}$，特别地： $d_1=a_1$。

那么显然差分数列的前缀和就是原数列。

只不过是把加变成减了而已。

那差分有什么性质呢，请大家自己探究。

我们很容易发现如果对一个数列区间加 $x$ 等价于对它的差分数列 $d$ 进行 $d_l+x$，同时$ d_{r+1}-x$（想一想，为什么）？

那么差分也很好理解。

差分一般会结合数据结构考察，这里略去例题，但一定要注意，这是处理区间加的一种有力手段。

定义二维数组 $a_{ij}$ 的前缀和 $S_{ij}$ 为 $\sum \limits_{l=1}^{i} \sum \limits_{r=1}^{j} a_{lr}$。

抽象的话就上图。

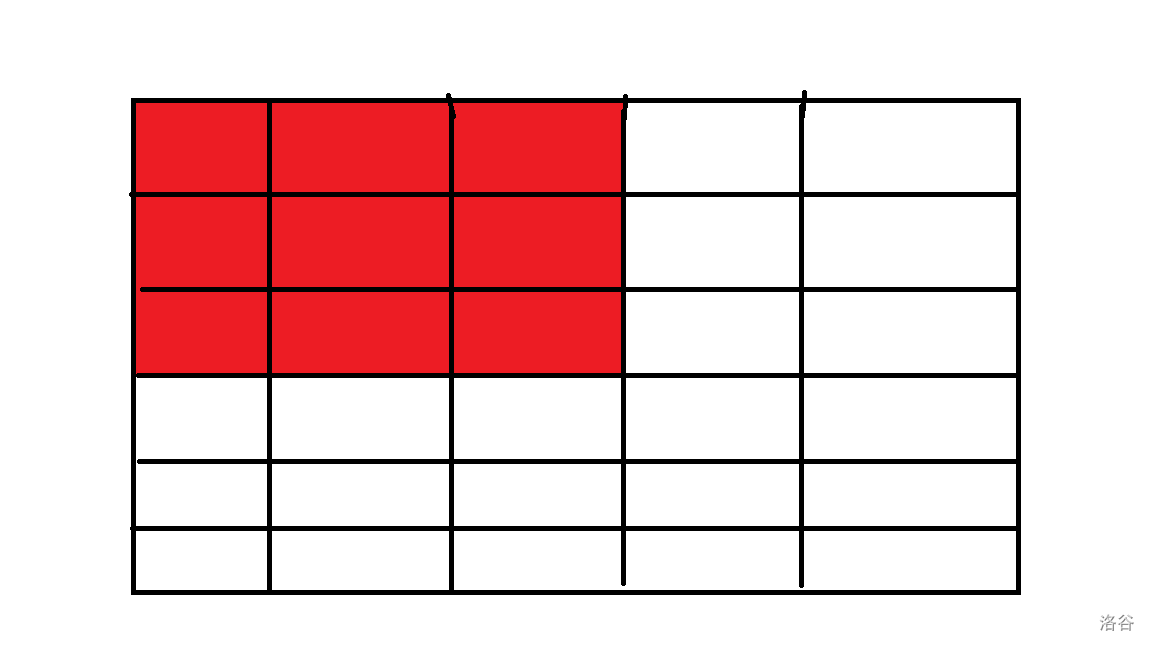
$S_{33}$ 就是图上标红的地方。

怎么求呢？

容斥原理！我们假设知道了所有小于 $i,j$ 的前缀和，那么看图来说：

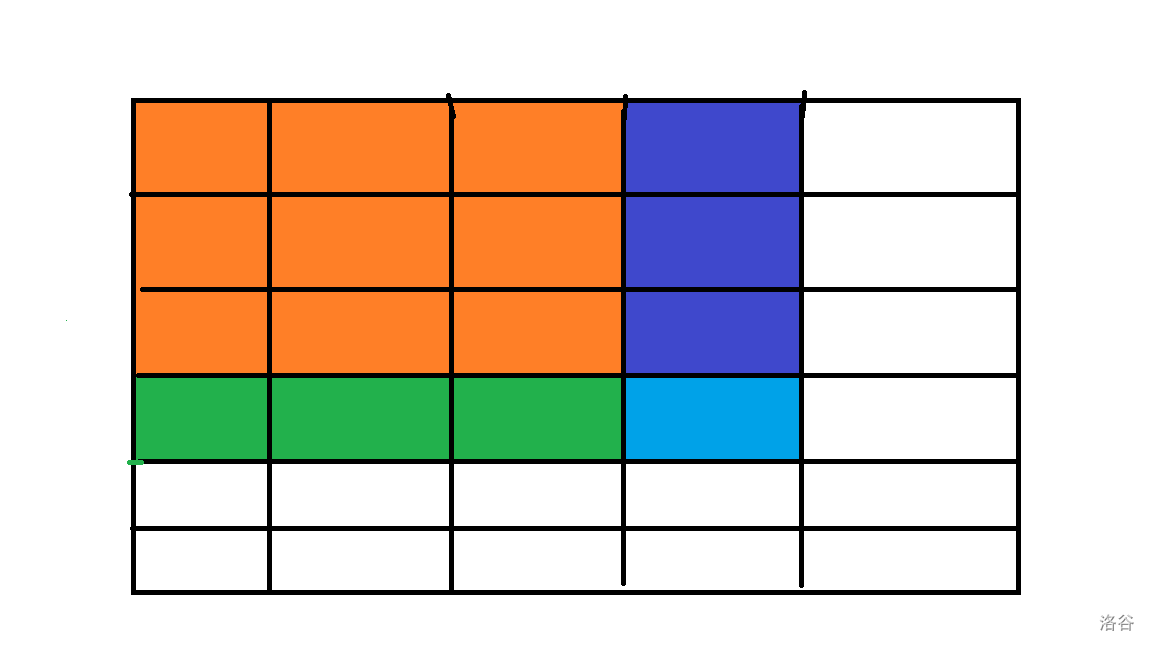
就是绿色+橙色+紫色+蓝色。而橙色就是 $S_{33}$，绿色就是 $S_{34}- S_{33}$，紫色就是 $S_{43}-S_{33}$ 。