zd的小窝
0%

CSP-J 2022补赛题解

发表于

植树节(planting)

一.一句话题意

区间加一，求序列最大值。

二.题目分析

一.线段树模板

略。

二.差分

定义：设原数组 $a_n$，设数组 $b_n=a_n-a_{n-1}$ 为 $a$ 的差分数组。其中一个性质是 $b$ 的前缀和数组就是 $a$。

我们很容易知道对 $a$ 任意区间 $[l,r]$ 区间加 $x$ 就等价于 $b_l + x$ 同时 $b_{r+1} -x$
证明略，请感性理解

三.代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		int l,r;
		cin>>l>>r;
		l++;r++;
		a[l]++;a[r+1]--;
	}
	for(int i=1;i<=1e6+4;i++){
		a[i]+=a[i-1];
	}
	int maxn=-1;
	for(int i=1;i<=1e6+4;i++){
		maxn=max(maxn,a[i]);
	}
	cout<<maxn<<endl;
}

宴会(banquet)

一.一句话题意

给定一个长为 $n$ 的序列 $a_n$ 和 $b_n$，求一个 $x_0$ 使得最小化 $\max_{i=1}^n{b_i+|x_i-x_0|}$。

二.题目分析

按照我们小学数学的知识，我们怎么处理绝对值问题呢？

其中一种解法就是几何意义：

我们先对这个式子进行等价变形，那么就有：

有点抽象？没关系来张图：

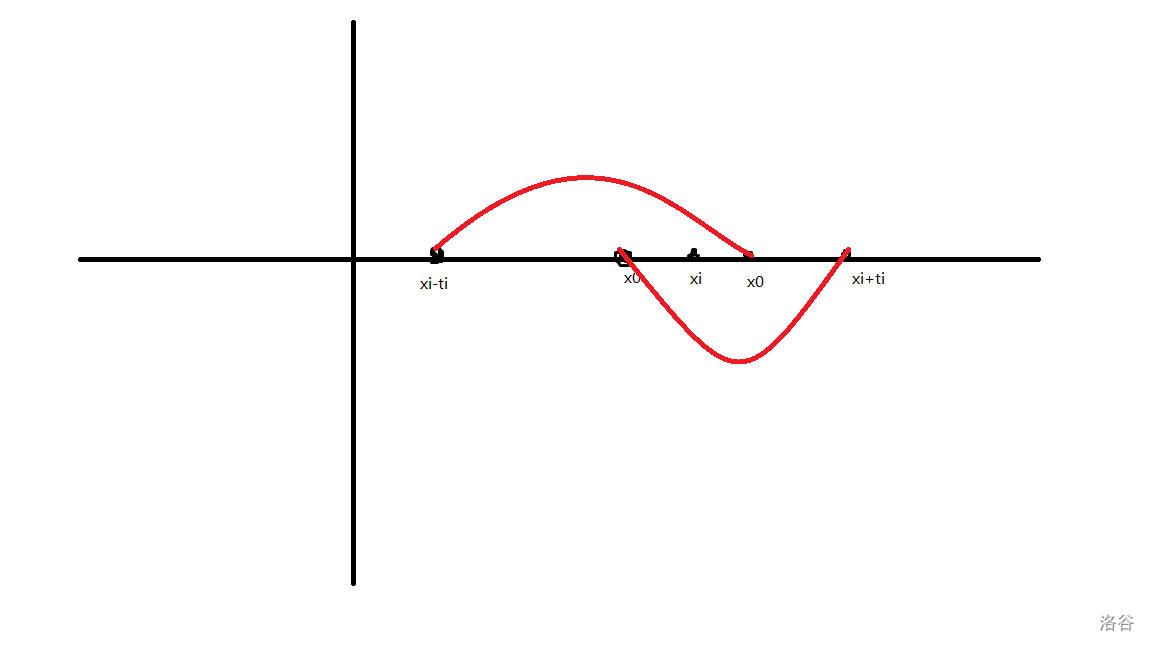
也就是说如果 $x_i<x_0$ 的时候，我们的 $d$ 就是右边红色的部分，否则就是左边红色的部分。

那么我们现在要让最大的 $d$ 最小 ，首先我们还是要找出这个 $d_{min}$。

那我们不妨找出值域，来看这样一张图：

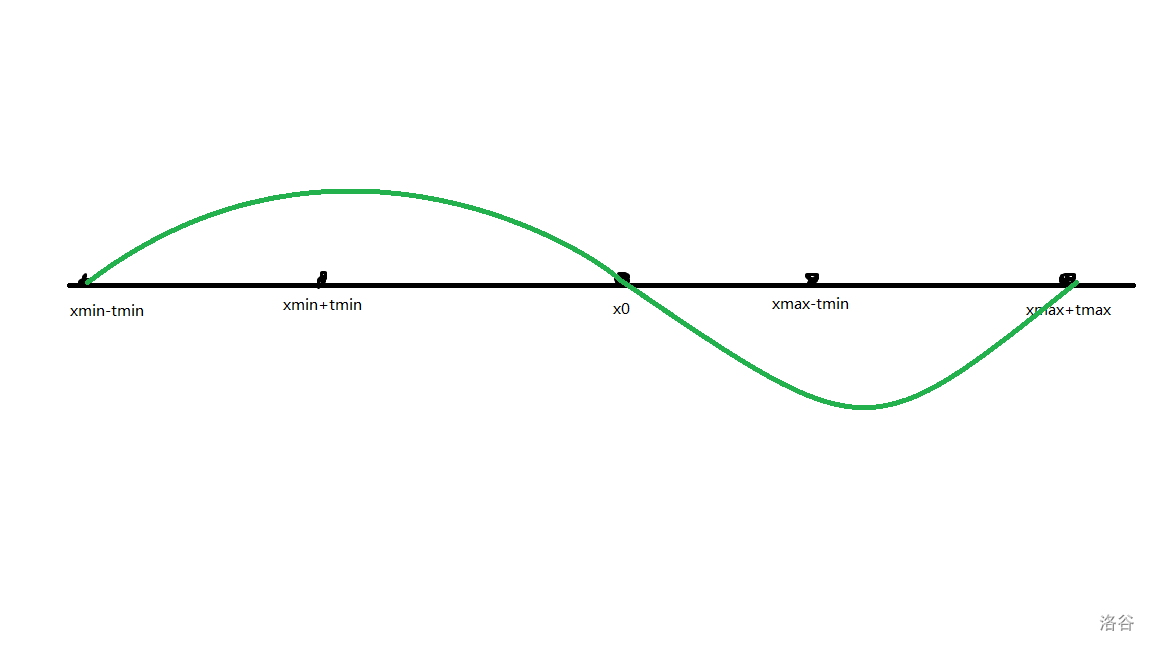
那么显然值域就是 $[x_{min}-t_{min},x_{max}+t_{max}]$。

那么显然当 $x_0$ 取值域终点的时候 $d=d_{min}$，即当 $\frac{x_{max}+t_{max}+x_{min}-t_{min}}{2}$ 即可。

代码时间

1
2
3
4
5
6
7
8
9
10
11
void solve(){
	read(n);
	for(int i=1;i<=n;i++)read(a[i]);
	for(int i=1;i<=n;i++)read(t[i]);
	int minn=INF,maxn=-1;
	for(int i=1;i<=n;i++){
		minn=min(a[i]-t[i],minn);minn=min(a[i]+t[i],minn);
		maxn=max(a[i]-t[i],maxn);maxn=max(a[i]+t[i],maxn);
	}
	printf("%.1lf\n",(minn+maxn)*1.0/2);
}

部署(deploy)

基础树论板子题。

一.题意简述

给定一棵树，两种操作：

1. 子树加
2. 父亲和儿子加

先进行操作，最后若干次单点询问。

二.题目分析

当我刚看到这道题的时候，我说：“这不是树剖板子？”接着我再看了一看发现不是，而且比树剖简单了不知道多少倍，毕竟是普及组的题目。

我们发现我们是修改完再查询，题目都把离线拍到了脸上。

考虑预处理操作最后再改，即最后只遍历一遍就可以知道所有点的权值。

首先是子树加，我们直接定义一个数组 $Sz_i$ 代表以 $i$ 为根的子树上加了多少，然后预处理就直接加就可以。

再接着是父亲和孩子的和，原题目给的是直接相连的点，但是这是一棵树，我们就要想一想树的特殊性质：树只有一个父亲、若干个儿子。

那只有一个父亲我们直接把父亲加上就好。

孩子呢？我们还知道树是一种递归结构，在这个题中就是指这些孩子都以这个节点为父亲。

那我们直接记录父亲加了多少，最后一遍 DFS 就可以知道每个点最后权值是多少了。

三.代码时间

  • 注意双向边别忘了开 $2$ 倍数组。
  • 题目中指定了 $1$ 号节点为根节点。
  • 代码只给出了核心部分。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/*
	Author:zd
	Status:WA on pretest 2
*/

void dfs1(int x,int f){
	fa[x]=f;
	for(int i=head[x];i;i=e[i].nxt){
		int y=e[i].to;
		if(y==f)continue;
		dfs1(y,x);
	}
}
void dfs2(int x,int tmp1,int tmp2){
	a[x]+=(tmp1+tmp2);
	for(int i=head[x];i;i=e[i].nxt){
		int y=e[i].to;
		if(y==fa[x])continue;
		dfs2(y,tmp1+sz[y],laz[x]);
	}
}

signed main(){
	read(n);
	for(int i=1;i<=n;i++)read(a[i]);
	for(int i=1;i<n;i++){
		int x,y;
		read(x,y);
		ade(x,y);
		ade(y,x);
	}
	dfs1(1,0);
	read(m);
	while(m--){
		int op,x,y;
		read(op,x,y);
		if(op==1){
			sz[x]+=y;
		}
		else{
			a[fa[x]]+=y;
			a[x]+=y;
			laz[x]+=y;
		}
	}
	dfs2(1,sz[1],0);
	read(k);
	while(k--){
		int x;
		read(x);
		writeh(a[x]);
	}
	return 0;
}



吟诗(poetize)

史上最难普及组题目

一.一句话简述不完题意

给定常数 $X,Y,Z$，求长度为 $n$ 的数列 $a(1\le a_i \le 10,1\le i \le n)$的个数， 使得存在 $1 \le x \le y \le z \le r $，使得：

是的我在尽量不抽象了。

二.题目分析

先想暴力。

显然有一个枚举全排列的暴力分，太过 $\color{red}\text{Native}$ 这里不说了。

$40$ 分呢？

我们想到去推柿子，但是问题是我们稍微写一写就发现我们直接这么做会出现重复计数的问题，并且这个问题还十分地棘手，怎么办呢？

我们发现总数量就是 $10^n$。正难则反，考虑解决不合法的数目，容斥原理即可。

然后便没有思路了，数学这条路算是堵死了。

再看一眼数据范围：$X+Y+Z \le 17 ,n \le 40$ 考虑状压 DP。

因为 $n$ 太大了我们考虑状压 $X+Y+Z$，现在的问题是设计一种状压方案储存一个不超过 $17$ 的数，同时还能快速判断条件是否合法。

我们考虑到把一个数 $m$ 拆成若干个有序正整数的方案数为 $2^{m-1}$ （想一想，为什么？），我们可以看成 $m$ 个 $1$ 相加，每一位中间可以选择分割或者不分割。受此启发，我们设计这样一种状态：第 $i$ 位若为 $1$ 说明在第 $i$ 位和第 $i+1$ 位之间选择分割，也就是说存在一个前缀和为 $i$ 。

然后我们再把它反转过来，变成后缀和，原因是我们 DP 是从前往后递推的，这样可以方便判断，具体来说，我们把 $17$ 分成 $5,7,5$，对应的压缩是 10000100000010000 ，从后往前数第 $5,12,17$ 位为 $1$，即存在 $5,12,17$ 的 后缀和。

怎么判断题意呢？只需要同时存在 $Z,Y+Z,X+Y+Z$ 的后缀和即可。

推一下柿子，当状态为 $i$时加入一个新数 $t$ 时，新的状态为 (i<<t)+(1<<(t-1))。

然后按照题意 DP 即可。

三.代码时间

  • 注意位运算的优先级很低，一定要勤加括号。
  • 一般这种题需要注意运算中爆 int ，本人习惯一般 #define int long long。
  • 取模一定要勤快，不然你都不知道你这个数为啥这么奇怪。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int n,m,k;
int f[45][N],X,Y,Z;
bool gb(int i,int x){
	return (x>>(i-1))&1;
}//取第 i 位 
bool check(int num){
	if(!gb(Z,num)) return 1;
	if(!gb(Y+Z,num)) return 1;
	if(!gb(X+Y+Z,num)) return 1;
	//后缀和判断是否不合法 
	return 0;
}

signed main(){
	read(n,X,Y,Z);
	f[0][0]=1;
	for(int i=1;i<=n;i++){//长度 
		for(int j=0;j<(1<<(X+Y+Z));j++){//枚举状态 
			for(int k=1;k<=10;k++){
				int u=(j<<k)+(1<<(k-1));//处理后缀和 
                u&=(1<<(X+Y+Z))-1;
				if(check(u))(f[i][u]+=f[i-1][j])%=mod;
			}//暴力填数 
		}
	}
	int ans=qp(10,n);
	for(int i=0;i<(1<<(X+Y+Z));i++)(ans+=mod-f[n][i])%mod;
	writeh(ans%mod);
	return 0;
}